The Mathematics of Zukofsky

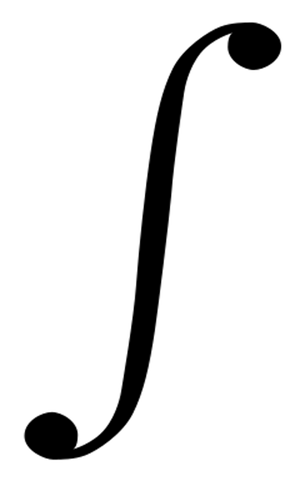
Check out this Scientific American blog post by Bob Grumman. In it, Grumman takes a deeper look at mathematics in poetry, focusing primarily on Louis Zukofsky's use of an integral sign, which:

appears in Zukofsky’s famous long poem, “A” (first published in 1969), which I won’t say much about–except that the fact that the quotation marks are part of the poem’s title should suggest to you a little of its expressive concern with matters as seemingly minor as punctuation marks.

According to Jeffrey Twitchell-Waas, the webmaster of Z-site: A Companion to the Works of Louis Zukofsky at http://www.z-site.net, who was kind enough to fill me in on what he knew of Zukofsky’s background in mathematics, Zukofsky “often said that he should have been an engineer–and that wasn’t just something he said later in life–recently I saw a letter from the early 1930s to (poet Carl) Rakosi (I think) where he says this. He went to the top math and science HS in NYC and later in the late 1920s he substitute taught there (presumably English) where he met Jerry Reisman as one of his students and who would become one of his best friends over the next decade plus.

Reisman was studying to be an electrical engineer and in the late 20s and early 30s LZ was reading some of his textbooks, such as on the new quantum physics. The mathematical formulas used in “A”-9, LZ always credited to Reisman. During the early 40s LZ worked for Reisman editing electrical technical manuals–the poem “It’s hard to see but think of a sea…” comes out of that. I haven’t run across much evidence that LZ read very deeply in mathematics and hard to say how much he picked up from Reisman. Obviously he felt he had an affinity with numbers and liked playing with formulaic possibilities, such as the tone row of “A”-20. But I doubt any of this is very sophisticated from the perspective of someone who knows a fair bit of math. But, also, I may simply be blind to what I don’t know. Don’t know if John Taggart or his thesis on LZ from the early 1970s would have/know more on this.”

I can’t quote the passage containing the integral sign because I’d have to sell my cat, Spike, to be able to afford the fee Zukofsky’s son, Paul, would charge me, and I don’t want to have to go to court to defend my use of it as scholar’s privilege, which I do believe it would be. I also sympathize with Paul’s reasons for charging what he does for any use of his father’s work. The core of his belief, as I understand it, is that academics quote famous writers’ work for material profit (not necessarily commercial profit but profit, nonetheless, via the tenure, increased salaries, etc., that they gain); hence, they should have to pay more than nominal rent on what they quote. If I didn’t think I could get by with a sort of paraphrase, though, I’d fight PZ to the Supreme Court!

Here’s the integral sign again. In Zukofsky’s poem, it has the word, “music,” just above its top, and the word, “speech,” just below its bottom.

According to the poem, this represents Zukofsky’s concept of poetry. The poem explains it as basically a continuum containing speech at one end and music at the other. More precisely, if much more clumsily, it means in calculus “the sum of all the infinitesimally-changing values of vocalization ascending from speech (at the lower limit) up to where it becomes music (at the upper limit).” Hence, it represents, “poetry as a patterned integration of words, beginning in speech and ending in music,” as my friend Sabrina Feldman (a, ahem, JPL source of help of mine) put it. (I also need to thank David Webb, a Dartmouth Math professor, who also gave me help.)

I feel it obligatory to discuss Zukofsky’s poem here for several reasons. The first is because of its historical importance (however little the poetry establishment has yet made of it). While mathematics has for a long time occasionally gotten into poetry (notably in the work of some of the 17th Century English metaphysical poets), so far as I know it has done so only as subject, not as actual expressive component–until Zukofsky’s poem. I therefore consider him the inventor of mathexpressive poetry. This, remember, I define as “poetry in which a mathematical operation (or a series of them) is carried out on non-mathematical terms, in the process adding significantly to the poem’s aesthetic value.”

Zukofsky’s poem (poem-within-a-poem, to be precise) is mathematically expressive due to the integral calculus operation a reader must carry out in order to understand it–or solve it, since Zukofsky makes it part of an equation by telling us the integral is what poetry equals. The derivative, “d(vocalization),” that should be included in the equation is implied, I should add, since it is infinitesimal values of vocalization’s non-semantic content that are integrated from zero, presumably to some much higher value, a hundred, say. That is, the continuum begins with highly verbal unmusical speech and ascends (and Zukofsky does want us to believe poetry is at its best when most musical) through less and less verbal vocalizations until it is minimally verbal, and maximally musical).

Much more of this fascinating piece to read here.